An illustrated description of the AES Standard

The competition announced by NIST had fifteen encryption algorithms submitted. The finalists included: Rijndael, RC6, Mars, Serpent, and Twofish.

After five years of thorough evaluation of the submitted projects, the victory was declared for the Rijndael algorithm, which officially became the federal standard in 2002 and simultaneously adopted a new name, AES. Resistance to cryptoanalytic attacks was not the sole determinant in these competitions. The criteria for assessing the submitted projects were as follows:

• General Security: tightly related to cryptoanalysis (including linear and differential) carried out by the cryptography community during the process of selecting the AES standard. Numerous articles published by the cryptography community on the proposed ciphers allowed for detailed assessment and exposed most of the strengths and weaknesses of the submitted algorithms.
• Software Implementations: for this criterion, features like execution speed, efficiency on different types of platforms and the correlation between execution time and key length played significant roles.
• Hardware Implementations: similar to software implementations, this criterion is linked to performance on various platforms (in this case, hardware, of course). Another crucial factor is the size of the program, which would obviously translate into an increase in potential costs in the case of hardware implementation.
• Adequacy of Limited Memory: This issue concerns specific cases of devices with very limited memory in which the evaluated ciphers were to be used (e.g., smart cards).
• Implementation Attacks: in this case, it is about resistance to attacks on the physical implementation of the algorithm. Examples of such attacks are: time attack or power analysis. The possibility of executing such attacks is related to the characteristics of the work of electronic systems - i.e. multiplication causes a greater load than addition, which translates into an increase in the power consumed by the system, just as writing a bit with the value 1 is more energy-intensive than writing a bit with the value 0, and the same applies to the time of performing individual operations.
• Encryption vs. Decryption: the difference between the encrypting and decrypting algorithm. The larger the difference between them, the larger the memory requirement for the entire implementation.
• Key Management Efficiency: this criterion applies to key exchange and sub-key calculations, or more precisely, the complexity and resource intensity of this process.
• Potential Usage of Parallel Computations: the possibility of the evaluated algorithm using parallel processing, which is increasingly popular these days, and any additional overhead associated with such computations.
• Versatility and Universality: this criterion mainly relates to the flexibility of the parameters accepted by the algorithm, namely, handling unusual block lengths, keys, and the ability to control the number of encryption rounds within the algorithm.

Rijndael became the first publicly available encryption algorithm approved by the NSA (National Security Agency) for protecting classified data. It was designed by Belgian cryptographs, Vincent Rijmen and Joan Daemen.

Rijndael is a block cipher that operates on 128-bit data blocks. It executes 10 (key 128 bits - standard adopted by NIST), 12 (key 192 bits), or 14 (key 256 bits) encryption rounds of substitution-permutation, each consisting of initial substitution, matrix permutation (row mixing and column mixing), and key modification. The substitution function's design makes the algorithm resistant to known differential and linear cryptoanalysis attacks.

Variants of the Rijndael algorithm, beyond the AES standard, perform 12 or 14 encryption rounds depending on the length of the key and data block.

The algorithm has been implemented in several programming languages. Additionally, the two main processor manufacturers - Intel and AMD - have introduced instruction sets accelerating data encryption and decryption with the Rijndael algorithm into their most recent series of processors back then ("Westmere" - Intel and "Bulldozer" - AMD).

So far, no cryptoanalytic attacks have emerged that could foretell the end of this standard. Most effective attacks are based on weaknesses in the implementation, not in the Rijndael cipher itself. Attack methods on the cipher itself still have a high computational complexity level, making their application impractical. Even quantum algorithms that pose such a great threat to RSA ciphers only slightly reduce the time of cryptanalytic attacks in the case of AES.

Let's take a closer look at how the Rijndael algorithm works. The following figure presents a vastly simplified block cipher operation diagram. At the input, we receive a data block of 128 bits length (16 bytes) and a key of 128, 192, or 256 bits length, which will be used to encrypt this data block.

Depending on the key length, the encryption process looks slightly different. As per the data contained in table below, the algorithm will execute 10 encryption rounds for an encrypting key of 128 bits length, 12 rounds for a 192-bit key, and 14 rounds for a 256-bit key.

The length of the key expansion also changes and must be equal to 16 bytes multiplied by the number of encryption rounds in the given variant, plus one. This is because, in addition to the standard encryption rounds, there is an additional operation that requires one more encryption subkey. In a highly simplified model, the encryption process using the Rijndael algorithm looks like the earlier diagram. The input plaintext is fed into the first round, along with the first encryption subkey. The output of the first encryption round becomes the input for the second encryption round, which processes it again using the second subkey. The result then moves to the third encryption round, and so on. At the output of the final encryption round, we obtain the final ciphertext produced by Rijndael. The next two subsections will provide a more detailed explanation of the encryption rounds, as well as the process of key expansion and the creation of subkeys for individual rounds.

A typical encryption round in the Rijndael algorithm consists of four operations: Subbytes, ShiftRows, MixColumns, and AddRoundKey. The illustration below presents both the encryption and decryption processes, using a 128-bit key and 10 rounds as an example. On the left side of this diagram, we see successive operations in the process of generating a ciphertext from input plaintext using an encrypting key, while the reverse process happens on the right side.

During both encryption and decryption, an additional AddRoundKey operation is called before the first round, and in the last round, there's no MixColumns/InvMixColumns operation. All transformations are performed on a 4x4 byte matrix known as a state matrix. Such a matrix is both the input and output for individual rounds of encryption as well as for individual transformations within the rounds themselves.

A simple transformation that binds the state matrix of a given encryption round with the appropriate round key. It involves executing XOR operation between corresponding bits of the state matrix values and the round key matrix values as illustrated in the following figure. AddRoundKey does not have a counter-transformation since it relies on the XOR operation, which is self-inverse. Thus, it occurs in both the encryption and decryption processes.

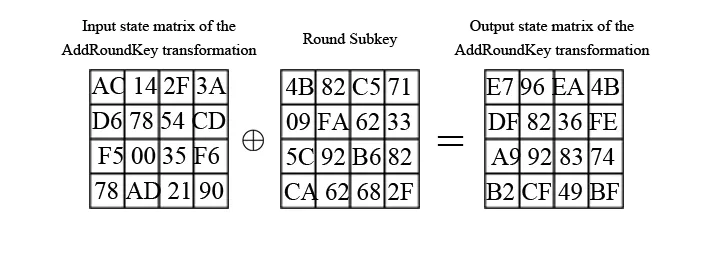
The AddRoundKey transformation is quite simple, but this does not affect the overall algorithm security, based on the complexity of the other transformations and the complexity of generating sub-keys for all rounds.

Like AddRoundKey, both these transformations are straightforward. The algorithm for the ShiftRows transformation is illustrated in the diagram below. The first row of the state matrix remains unchanged, the second one rotates cyclically to the left by one byte, the third by two bytes, and the fourth by three bytes, respectively.

The inverse transformation, i.e., InvShiftRows, involves performing similar rotations in the opposite direction.

These simple transformations significantly impact the overall algorithm's safety. They scatter the column content across all four columns, thereby performing 'column disintegration' and removing dependency that could support a cryptographic attack.

The Subbytes transformation is essentially a simple substitution based on a so-called Substitution Box (S-Box in short). An S-box is a 16x16 byte matrix represented in the following illustration. The transformation proceeds as follows: the input byte is divided into two parts, the four most significant bits determine the S-Box matrix row, and the four least significant bits ascertain the S-Box matrix column. For instance - the mapping of a byte with a value of 5B results in a byte of 39.

In decrypting the process in the InvSubbytes transformation, an IS-Box is applied (shown in further illustrations), performing the inverse transformation and restoring original values. Thus, for the previously mentioned byte of 39, the InvSubbytes transformation will yield a value of 5B.

Neither the S-Box nor the IS-Box are random products. If they were, decryption would be impossible. Both matrices are generated by a deterministic algorithm. This means that for implementations without memory restrictions, the S-Box and IS-Box can be generated much earlier (or be included in the program) and used repeatedly.

The main purpose of this transformation is to provide low correlation and non-linear dependence between input and output bytes, which significantly increased resistance to potential linear cryptoanalysis attacks. Despite speculation that the S-Box and IS-Box were chosen to have a hidden backdoor, no one has yet provided evidence of this.

MixColumns operation is performed independently for each column using the formulas stated below (s represents the original value while s' stands for the value after transformation):

However, it's worth recalling that these equations perform multiplication according to the rules of this operation over the finite field GF(2^8). The XOR operation appearing in these equations can also be depicted as the corresponding addition operation over the finite field GF(2^8). Both MixColumns and the reverse operation InvMixColumns are presented below.

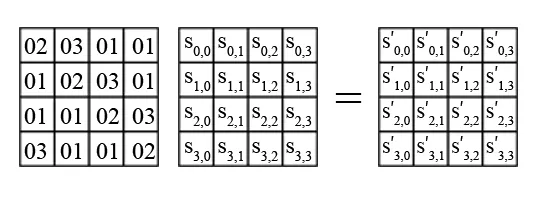
The main purpose of this transformation is to make every column dependent on the others and shuffle the bits within each byte of the state matrix.

These four transformations complete a typical (excluding the last one, which doesn’t contain the MixColumns and InvMixColumns operations) encryption/decryption round. The figure below presents a single, full Rijndael encryption round sequence:

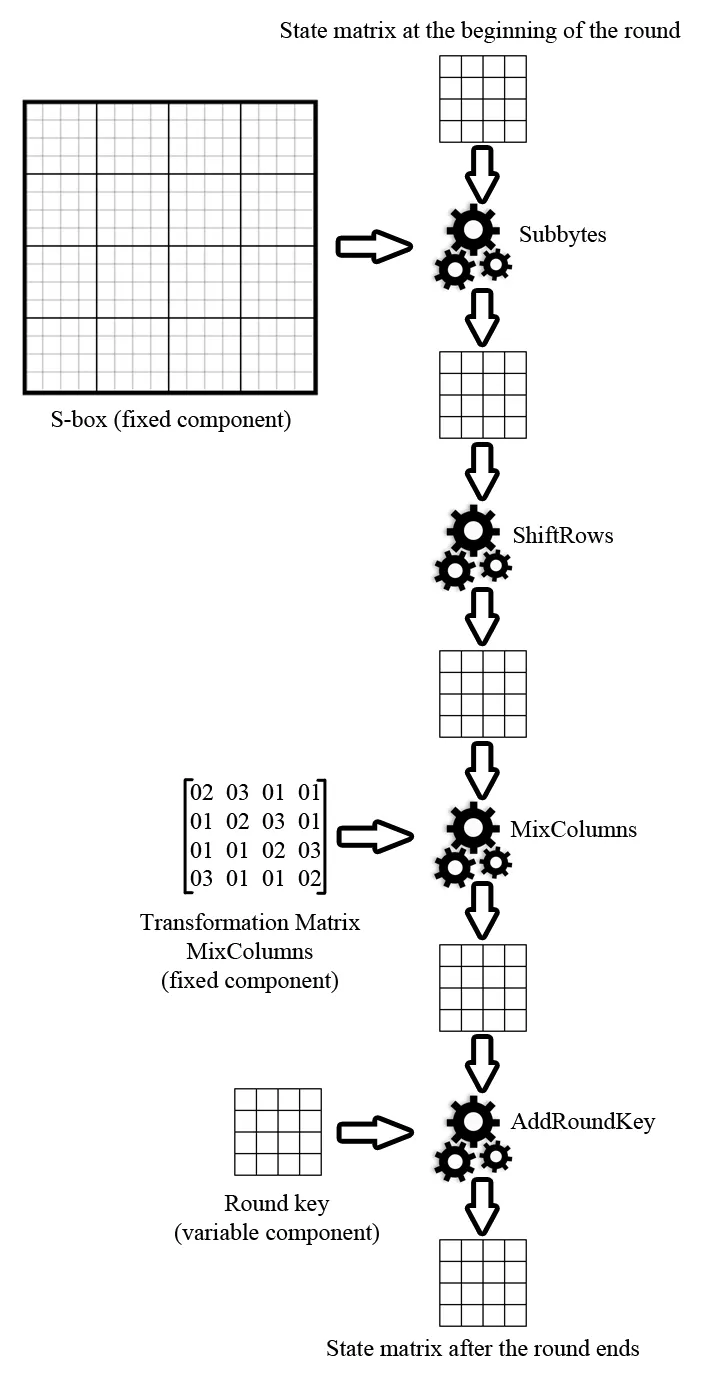
At the beginning of a round, a 4x4 byte matrix is provided. This undergoes the substitution transformation (Subbytes) using the S-Box matrix. The result is a new state matrix which goes through row shifting in accordance with the characteristics of the ShiftRows transformation. Another state matrix is obtained and it gets passed onto the MixColumns function where it undergoes multiplication over the GF(2^8) field by the previously mentioned Sbox matrix. The final stage involves performing an XOR operation between the consequent values of the previously obtained state matrix and the subkey matrix obtained from the key expansion process for the given encryption round (AddRoundKey transformation).

The process of generating subkeys starts by copying the contents of the key into the first four words of resultant vector W. These four words serve as a seed that will be used to generate the remaining 40 words constituting the subkeys for the subsequent ten encryption rounds. As can be concluded from the contents of the figure below, the calculated content of any word w[i] depends on its preceding words w[i-1] and w[i-4]. Calculating three of the contents is restricted to a straightforward XOR operation as seen in the illustration. Every fourth value is more difficult to obtain and requires calculating the function ‘G’, visible in the following scheme.

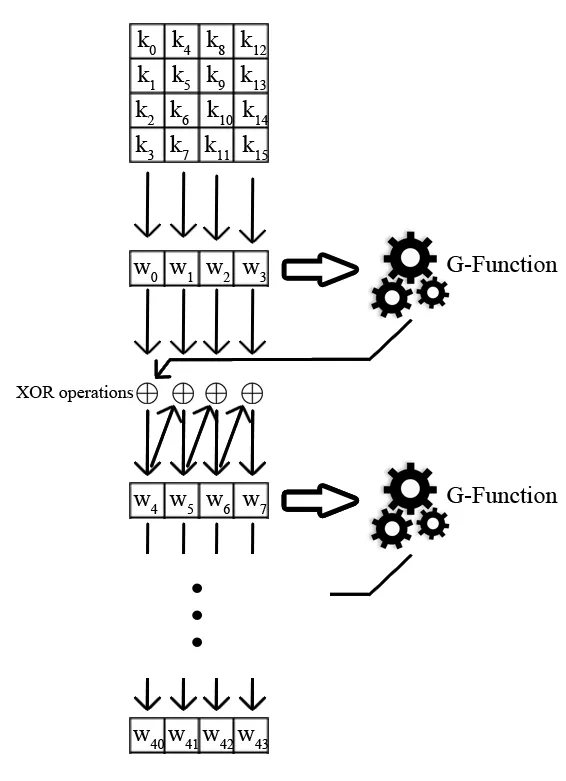
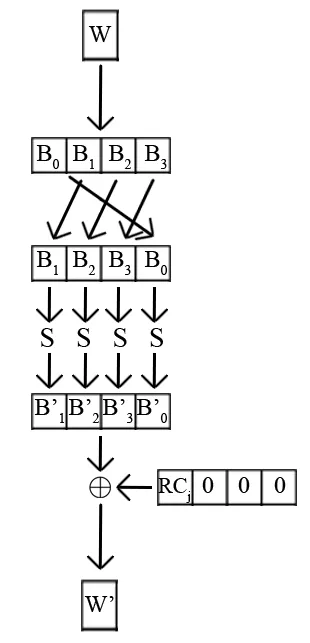
Let’s take a moment to analyze the G function. The first operation rotates a word to the left by one byte (RotWord operation). The second operation carries out substitutions using the already presented S-Box, which is a version of Subbytes operation referred to as SubWord.

The final step consists of symmetrically adding the results of the above two operations with the round constant Rcon[n] (for the nth round). Rcon has a specific structure - only the first word (eight most significant bits) has a value, the other three words are all zeros. The first word is obtained from the formula RC[1] = 1, RC[n] = 2 * RC[n-1]. The formula is calculated over the GF(2^8) field, so the consequent values for the ten encryption rounds are: 01, 02, 04, 08, 10, 20, 40, 80, 1B, and 36.

The key generation process is crucial for the strength of the Rijndael algorithm. Thanks to its structure, especially the operations performed within the G function, virtually no similarities exist between subsequent subkeys for encryption rounds. Furthermore, the key generation algorithm has other advantages. A significant portion of the subkey bits cannot be calculated based on partial knowledge of the main key or full subkey of one round. This algorithm's implementation is relatively simple and efficient, which carries its importance.

To sum up the Rijndael/AES algorithm in a few sentences, we need to highlight the general simplicity of this algorithm. No vast mathematical background is needed to understand the process of generating ciphertext using AES. Herein lies its strength. If an algorithm is excessively complex and complicated, fewer people are prone to examine it closely. Moreover, excessive complexity often carries the risk of various hidden dependencies, which very often is the starting point for effective cryptanalytic attacks.