General Overview of Cryptographic Algorithms

In today's digital world, securing sensitive data is more critical than ever. Whether it's protecting personal communications, securing financial transactions, or ensuring the integrity of online systems, cryptographic algorithms play a fundamental role in modern cybersecurity. These algorithms provide the backbone for secure communication, authentication, and data integrity, enabling trust in an increasingly interconnected world.

This blog post explores key cryptographic techniques, including Symmetric Ciphers, Asymmetric Ciphers, Stream Ciphers, Block Ciphers, One-Way Hash Functions, and Digital Signatures. Each of these plays a distinct role in encryption, authentication, and data protection. Understanding how they work and their differences is essential for anyone interested in cryptography, cybersecurity, or data privacy. Some of these cryptographic algorithms will be detailed in separate posts on our blog.

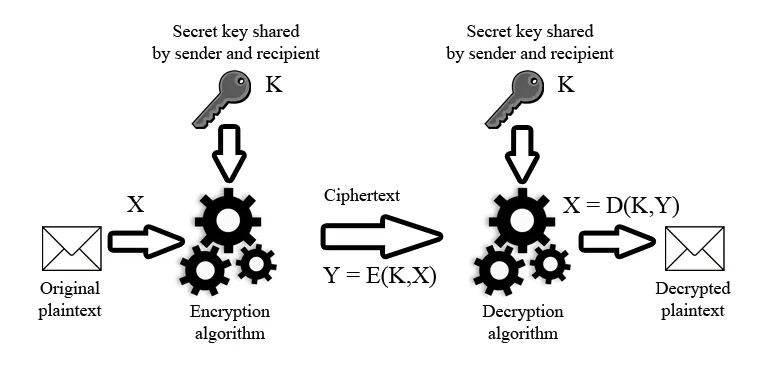
Symmetric encryption, also known as conventional encryption, involves both encrypting and decrypting data using the same key. Diagram below presents a conceptual model of the symmetric encryption process. The encryption algorithm E transforms the original plaintext X into ciphertext Y using a secret key K. The decryption algorithm D is the reverse of the encryption process, and by applying the same key K to the ciphertext Y, the original plaintext X is restored.

Historically, symmetric encryption is based on two techniques: substitution and transposition. Substitution methods (e.g., monoalphabetic, polyalphabetic, or homophonic) replace elements of the plaintext with elements of the ciphertext, while transposition methods (e.g., the Greek Scytale) rely on systematic rearrangement of plaintext elements.

Modern symmetric ciphers include Twofish, Serpent, AES (presented in our article An illustrated description of the AES Standard), Blowfish, RC4, 3DES, and IDEA NXT.

Asymmetric encryption, more commonly known as public-key encryption, is a type of cryptosystem in which encryption and decryption are performed using two different keys: a public key and a private key.

The diagram below presents a simplified model of asymmetric encryption using a public key. When communication is established, interdependent key pairs are generated—a public key K and a private key P. The sender encrypts the original plaintext X using an encryption algorithm E, transforming it into ciphertext Y with the recipient’s public key K. To read the message, the recipient applies the decryption algorithm D with their private key P, which corresponds to the shared public key K. This process restores the original plaintext X.

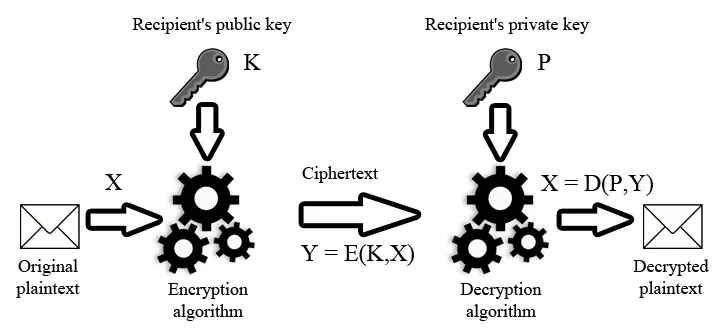
This method ensures confidentiality since only the holder of the private key can decrypt a message encrypted with the public key. The process can also work in reverse—the sender can encrypt a message using their private key. In this case, anyone with access to the corresponding public key can decrypt it, proving that the message comes from a trusted source (authentication). This scenario is commonly used in digital signatures.

Asymmetric cryptography is a relatively recent invention. The officially recognized inventors of this encryption method are civilian researchers Martin Hellman and Whitfield Diffie, who published their findings in 1976. However, two years earlier, Ralph Merkle proposed a key exchange algorithm, and the history of asymmetric ciphers dates even further back. The NSA had already taken an interest in such concepts as early as the 1960s.

Today, the most widely used public-key cryptosystem is RSA, named after its inventors—Ron Rivest, Adi Shamir, and Leonard Adleman. Its security relies on the computational difficulty of factoring large composite numbers. Another noteworthy encryption method, though less popular than RSA, is Elliptic Curve Cryptography (ECC), which derives its security from the complexity of computing discrete logarithms on elliptic curves. ECC provides security comparable to RSA but with significantly shorter key lengths and higher efficiency.

Modern asymmetric encryption algorithms include RSA, ElGamal, and ECDH.

The process of stream encryption is performed bit by bit or byte by byte. Each successive bit of the plaintext input stream Pi is transformed by the encryption algorithm (which can be as simple as an XOR operation) using the corresponding bit from the key stream Ki, resulting in the ciphertext stream Ci. During decryption, the ciphertext bits Ci pass through the decryption algorithm, which, using the same key stream Ki, restores the original message Pi.

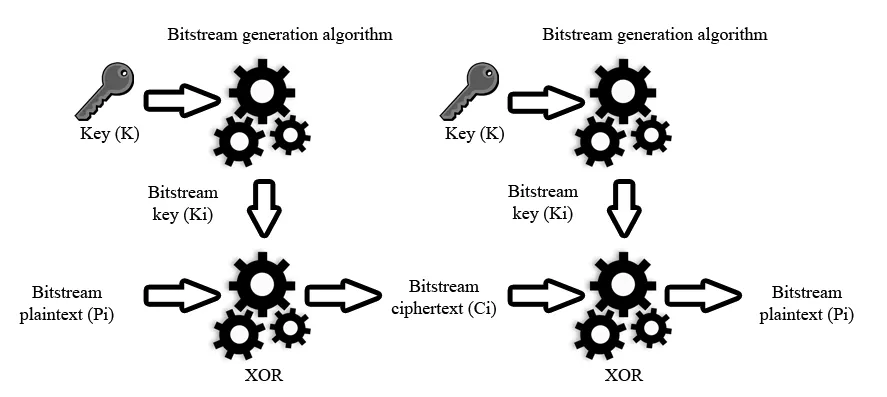
The weakest point of the stream encryption model is the algorithm responsible for generating the key stream Ki from an initial value known as the key K. Such algorithms are necessary for practical implementations of stream ciphers. In an ideal theoretical case, this step could be eliminated, but that would require the key to be as long as the message itself. While this guarantees perfect security as long as the key remains secret, it is a major limitation. This model is known as the One-time pad, originally proposed by Gilbert Vernam.

In practice, pseudorandom number generators (PRNGs) are used to extend a relatively short key K (serving as a seed) into a much longer key stream Ki, which is then used to encrypt the message. To ensure security, such algorithms must meet several criteria. First, the generated stream should resemble a truly random distribution as closely as possible. Additionally, it should not reveal any information about the original key K used as the seed for generating Ki and should be as unpredictable as possible.

Classic examples of stream ciphers include the autokey Vigenère cipher and the previously mentioned Vernam One-time pad.

Modern stream ciphers include RC4, Salsa20, SNOW, and SOSEMANUK.

As shown in the diagram below, a block cipher treats individual plaintext blocks M as separate entities and, through a series of transformations, produces a ciphertext C of the same length—n bits—as the original plaintext M. Typically, block sizes of 64 or 128 bits are used. Similar to stream ciphers, both parties in the communication share the same key K. The decryption process is simply the reverse of encryption—by inputting the ciphertext C and the key K into the algorithm, the original plaintext M is restored.

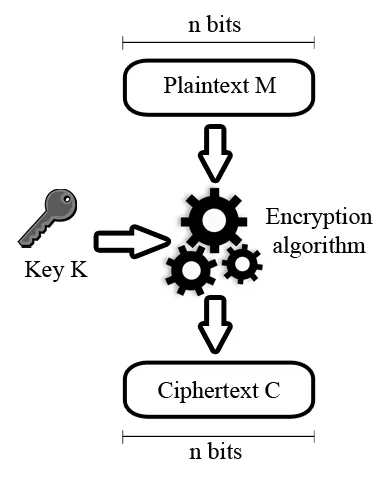
By using different operating modes, such as Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB), block ciphers can achieve effects similar to those of stream ciphers.

A great deal of research has been dedicated to studying the properties of block ciphers. In general, they are more widely used than stream ciphers, as most network applications implementing symmetric encryption rely on block ciphers rather than stream ciphers.

Modern block ciphers include AES, Camellia, Serpent, and Twofish.

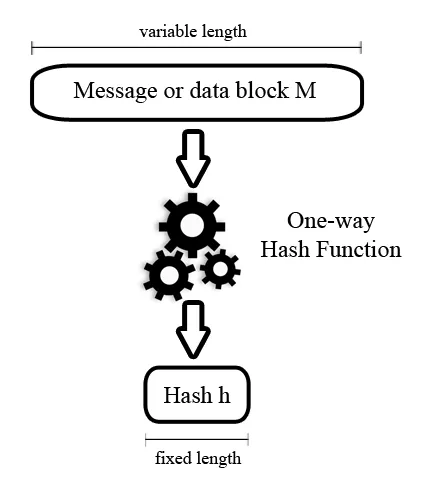
A hash function H transforms a message or data block M of any length into a fixed-length value h, known as a hash. This type of cryptographic algorithm must be deterministic, meaning that the same input must always produce the same output. To be considered suitable for cryptographic applications, a hash function must meet several important criteria.

First and foremost, as the name suggests, it must be one-way (irreversible)—it should be impossible to derive the original input M from the hash h. Even the smallest change in the input data M must result in a significant difference in the output hash h (a property known as the avalanche effect). Additionally, the probability of two different inputs M producing the same hash value h (a collision) must be as low as possible.

Modern hash functions include BLAKE3, SHA-256, SHA-3, and Whirlpool.

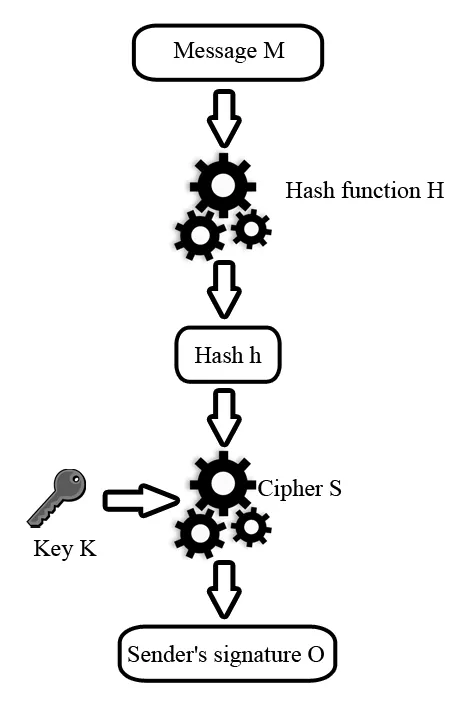
A digital signature is not an encryption algorithm in itself, but it is a powerful mechanism with broad applications. A digital signature is an authentication method that allows the sender of a message to attach data serving as a signature, which verifies the authenticity of the message. The process of working with a digital signature can be divided into two parts: signature generation by the message sender and signature verification by the recipient or other interested parties.

The diagram below illustrates the signature generation process. The sender first generates a hash h of the message M using a hash function H. Then, using their private key K and an asymmetric encryption algorithm S, the sender encrypts the hash to create the digital signature O. This signature is then attached to the message M.

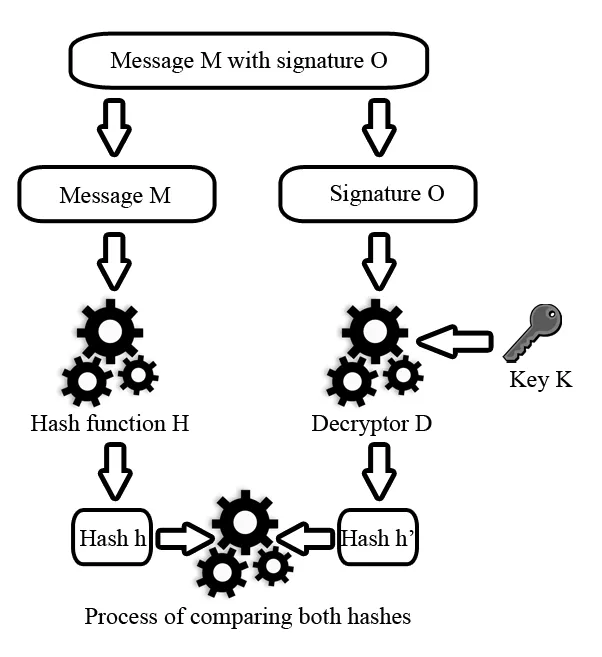
The next diagram shows the signature verification process. First, the message M and its signature O are separated. The message M is processed using the same hash function H that was used during signature generation, producing the hash h. Meanwhile, the signature O is decrypted using the recipient’s asymmetric decryption algorithm D and the sender’s public key P, resulting in a hash h′. If h≠h′, this indicates that either the message content or the digital signature has been tampered with.

The Digital Signature Standard (DSS) is a widely accepted standard for digital signatures, approved by NIST (National Institute of Standards and Technology). It utilizes hash functions such as SHA-1 or SHA-2.

This post provides a comprehensive overview of cryptographic algorithms, covering symmetric and asymmetric encryption, stream and block ciphers, hash functions, and digital signatures. Each type of algorithm has distinct strengths and applications, and when combined, they form robust cryptographic systems.